Using Plotly to visualize American Fraud Analytics¶

March 2019

By Joe Ganser

Abstract¶

In this research, a model is made that estimates the number of crimes of various types committed in each state, and calculates the probability of a citizen comitting a given type of crime for each state. The focus is on fraud crimes. The model uses arrest statistics for various crimes in each town of each American state, and aggregates them to make conclusions about the larger population. The model is validated by examining how it estimates the frequency in which arrests are made for other crimes. This project was constructed in Python 3.

I. Introducing the data¶

The data used for this analysis was based upon crime stats reported to the FBI in 2015. Before cleaning it had 5874 rows, where each row represented a town. After cleaning, 3664 rows (towns) were left distributed across 37 US states. This covered a population of 60 million citizens, and 54 different types of crimes.

The cleaned, model ready data had the following structure;

states	City	Population	total_crimes	Aggravated Assault	Simple Assault	Intimidation	Murder and Nonnegligent Manslaughter	Negligent Man- slaughter	Justifiable Homicide	Kidnapping/ Abduction	Rape	Sodomy	Sexual Assault With an Object	Fondling	Sex Offenses, Non- forcible	Statutory Rape	Arson	Bribery	Burglary/ Breaking & Entering	Counter- feiting/ Forgery	Destruction/ Damage/ Vandalism of Property	Embezzle- ment	Extortion/ Blackmail	False Pretenses/ Swindle/ Confidence Game	Credit Card/ Automated Teller Machine Fraud	Imper- sonation	Wire Fraud	Pocket- picking	Purse- snatching	Shop- lifting	Theft From Building	Theft From Coin Op- erated Machine or Device	Theft From Motor Vehicle	Theft of Motor Vehicle Parts or Acces- sories	All Other Larceny	Motor Vehicle Theft	Robbery	Stolen Property Offenses	Drug/ Narcotic Violations	Drug Equipment Violations	Por- nography/ Obscene Material	Pros- titution	Assisting or Promoting Prostitution	Weapon Law Violations
ALABAMA	Hoover	85163.0	4627.0	52.0	539.0	201.0	3.0	0.0	0.0	3.0	17.0	6.0	0.0	9.0	0.0	0.0	1.0	0.0	306.0	63.0	231.0	54.0	0.0	43.0	199.0	111.0	0.0	3.0	1.0	917.0	348.0	0.0	471.0	101.0	244.0	76.0	51.0	28.0	334.0	148.0	7.0	15.0	0.0	45.0
ARIZONA	Apache Junction	38519.0	2964.0	82.0	345.0	64.0	0.0	0.0	0.0	3.0	2.0	0.0	1.0	45.0	2.0	2.0	7.0	0.0	352.0	29.0	528.0	0.0	0.0	65.0	32.0	62.0	0.0	0.0	0.0	336.0	10.0	0.0	99.0	22.0	381.0	102.0	11.0	10.0	155.0	166.0	4.0	0.0	10.0	37.0
ARIZONA	Gilbert	247324.0	8676.0	121.0	846.0	202.0	2.0	1.0	1.0	48.0	27.0	1.0	0.0	50.0	20.0	20.0	20.0	0.0	519.0	82.0	1592.0	18.0	6.0	162.0	149.0	278.0	0.0	1.0	3.0	832.0	96.0	0.0	751.0	64.0	903.0	137.0	32.0	76.0	701.0	845.0	13.0	10.0	1.0	46.0
ARIZONA	Yuma	93923.0	7985.0	330.0	668.0	167.0	5.0	1.0	0.0	33.0	35.0	10.0	1.0	59.0	11.0	11.0	32.0	1.0	680.0	37.0	1713.0	19.0	3.0	278.0	122.0	176.0	12.0	5.0	5.0	752.0	101.0	23.0	344.0	115.0	742.0	270.0	75.0	22.0	467.0	573.0	13.0	0.0	0.0	74.0
ARKANSAS	Alma	5581.0	661.0	16.0	129.0	84.0	0.0	0.0	0.0	2.0	1.0	5.0	0.0	0.0	0.0	0.0	0.0	0.0	35.0	10.0	85.0	0.0	0.0	0.0	15.0	8.0	1.0	1.0	1.0	64.0	17.0	0.0	34.0	2.0	108.0	6.0	2.0	5.0	18.0	6.0	1.0	1.0	0.0	4.0

Aside from states,town,Population,total_crimes, each column represents the number of arrests made for the given crime in that town in the year of 2015.

II. Problem Statement & Goals of the Analysis¶

The goal is to make a deicison as to which states have the lowest probability of someone comitting a fraudulent act. This allows for insurance companies to make marketing decisions on which states to work with so they minimize their risks. The problem is calculating the probability of a person comitting fraud from each state.

The general approach behind the model is one that is mathematically based, integrating basic probability theorems. No machine learning is needed to solve this problem, and and it would be surprising if anyone used it.

There are several goals;

Create a model to produces the probability of a person in a given state comitting fraud
Rank states by probability of a citizen comitting fraud (find the lowest 5)
Visualize a heatmaps of crime distributions
Estimate and validate the rate at which arrests are made for crimes.
- And compare it to known rates (e.g. credit card fraud).

Using the listing of arrests for each crime in each town of a state, we are to estimate the number of frauds that happen in each state. Using that, we calculate the probability of a person comitting fraud by dividing by the population of the state.

III. Model Construction and theory¶

The model used in this analysis is based upon probability theory and making estimations of how many crimes of a given type their are in each town of each state. Then, all the estimates for each town are summed to find the total for the given state. After that, this number is divided by the number of people in the state (all the towns studied) to find the probability of the given crime per person.

Mathematical Construction

The derivation begins with Baye's theorem;

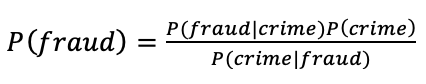
This says the the probability of fraud (or any crime) depends upon the Baye's relation of the probability of fraud given the distribution of other crimes.

Because a fraud by definition is a crime, the probability of an event being a crime being a fraud is one, i.e.

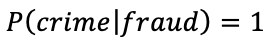
So this leads to;

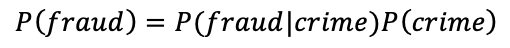
And if we give the definitions;

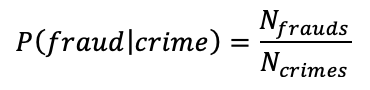
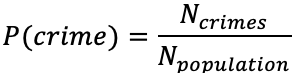
Therefor;

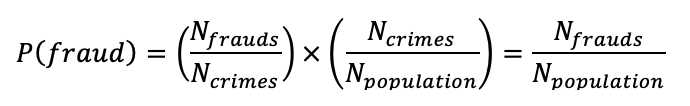
Where N_population is the number of people in the population studied. By what is the actual number of frauds? Is is just the number of arrests? We assume the actual number of frauds in existence exceeds the number of arrests for fraud;

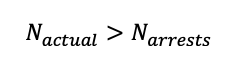
We focus on calculating the actual number of frauds in each town. Using the records of arrests for other crimes in the town, we sum them all up with a weighting system. i.e.

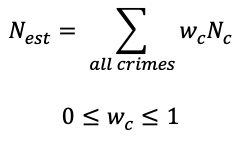
Now the critical portion of the model comes into play - calculating the weights. The weights are calculated using the correlation coefficients of each other crime with the fraud crime we're studying

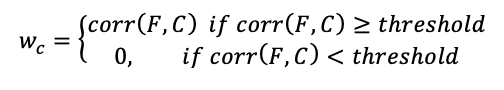
So we have a threshold for the correlation. This means that we set the weight equal to the correlation between a given crime and fraud if its greater than a threshold value, and set it equal to zero if its not.

Now that an estimation is made for the number of frauds in a given town, we sum over all the towns in the state. To find the probability of fraud per person, we simply divide by the population of the state.

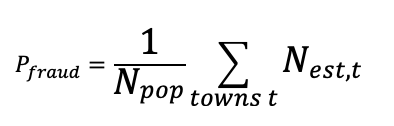
Where N_est,t is the estimated number of frauds in town t. This model can also be used estimate over all frequency at which arrests are made for crimes. This is done as follows.

First we sum over all the estimated number of frauds for all the towns in the USA;

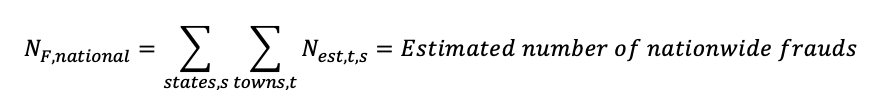
Then we sum over all the arrests for frauds, nationwide.

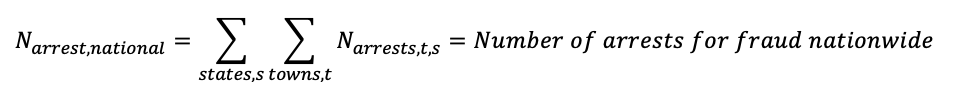
And the probability is then;

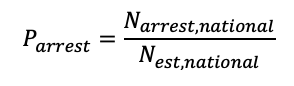
Which is the probability of making arrest for a given fraud (or other crime).

We'd expect the probability of an arrest made for a credit card fraud to be very low. We shall see the model produces these results.

Model Code in Python

The model code is built into a function. It's input is the cleaned data, the crimes we want to study and a threshhold correlation coefficient. The ouput is a dataframe and the nationwide rate (probability) at which arrests are made for the given crime.

def model(data,fraud_crimes,threshold):
    df = data.copy()
    import warnings
    import numpy as np
    warnings.filterwarnings('ignore')
    states = df['states'].unique() 
    #group all the fraud crimes together
    if len(fraud_crimes)>1:
        df['fraud_count'] = df[fraud_crimes].sum(axis=1)
        df.drop(fraud_crimes,axis=1,inplace=True)
    else:
        df['fraud_count'] = df[fraud_crimes[0]]
        df.drop(fraud_crimes,axis=1,inplace=True)


    combined_frame = pd.DataFrame()

    #loop over each state
    for state in states:
        dummy_frame = df[df['states']==state]
        #if the number of towns in the state is greater than the total number of crimes in the dataset (56),
        #use the correlation coefficients of each crime for only that state
        if len(dummy_frame)>=56:
            correlations = pd.DataFrame(dummy_frame.corr()['fraud_count']).reset_index()
            correlations['fraud_count'] = correlations['fraud_count'].apply(lambda x: x if x>=threshold else 0)
            correlations['crime'] = correlations['index'].apply(lambda x: 1 if x in crimes+['fraud'] else 0)
            correlations = correlations[correlations['crime']==1].drop('crime',axis=1)
            for i in correlations.index:
                factor = correlations.loc[i]['fraud_count']
                feature = correlations.loc[i]['index']
                if feature not in ['total_crimes','fraud_count']:
                    dummy_frame[feature] = dummy_frame[feature].apply(lambda x: factor*x)

        elif len(dummy_frame)<56:
        #if the state has less than 56, use the correlation coefficients for the entire country
        #to calculate the weights.
            correlations = pd.DataFrame(df.corr()['fraud_count']).reset_index()
            correlations['fraud_count'] = correlations['fraud_count'].apply(lambda x: x if x>=threshold else 0)
            correlations['crime'] = correlations['index'].apply(lambda x: 1 if x in crimes+['fraud'] else 0)
            correlations = correlations[correlations['crime']==1].drop('crime',axis=1)

        for i in correlations.index:
            factor = correlations.loc[i]['fraud_count']
            feature = correlations.loc[i]['index']
            if feature not in ['total_crimes','fraud_count']:
                dummy_frame[feature] = dummy_frame[feature].apply(lambda x: factor*x)
        combined_frame = pd.concat([combined_frame,dummy_frame],axis=0)

    model_groupby = combined_frame.groupby('states').sum().reset_index()
    model_groupby_crimes = [i for i in model_groupby.columns if i not in ['states','Population','total_crimes']]
    model_groupby['est.Frauds'] = model_groupby[model_groupby_crimes].sum(axis=1)
    model_groupby['%est.Caught'] = model_groupby['fraud_count'].div(model_groupby['est.Frauds'],axis=0).multiply(100)
    model_groupby = model_groupby[['states','Population','total_crimes','fraud_count','est.Frauds','%est.Caught']]
    model_groupby['fraud_prob'] = model_groupby['est.Frauds'].div(model_groupby['Population1'],axis=0)
    model_groupby.sort_values(by='fraud_prob',ascending=True,inplace=True)

    model_groupby = model_groupby[['states','fraud_prob','Population','total_crimes','fraud_count','est.Frauds','%est.Caught']]
    model_groupby = model_groupby.reset_index().drop('index',axis=1)


    nation_wide_arrests = model_groupby['fraud_count'].sum()
    nation_wide_estimates = model_groupby['est.Frauds'].sum()
    percent_caught = round(100*nation_wide_arrests/nation_wide_estimates,2)

    print('crimes analzed: ',fraud_crimes)
    print('Nation wide % of crimes where arrests are made',percent_caught,'%')
    print('Nation wide arrests :',round(nation_wide_arrests))
    print('Nation wide estimate number of crimes: ',round(nation_wide_estimates))
    return model_groupby

IV. Key Results¶

The main objective was to find the states with the lowest rate of fraud instances. To solve this problem, all fraud related crimes in the data were aggregated together to be represented as one crime. These crimes included the following labels in the data;

FalsePretenses/Swindle/ConfidenceGame
CreditCard/AutomatedTellerMachineFraud
Imper-sonation
WelfareFraud
WireFraud
Counter-feiting/Forgery

Throughout this analysis, any time a 'fraud crime' is referred to, it referrs to a person comitting any of these crimes.

Nationwide, it was found that about 7.37% of these crimes (aggregated) led to an arrest. There were a total of 302,783 fraud related arrests in the USA in 2015, recorded from a population of 60.2million residents.

IV.A Validating the model

Any useful model should produce results that are realistic. How could can this model be evaluated to determine if it's a good fit? In this case, we use the predicted rate at which arrests are made for varying crimes to see if it's realistic.

It's widely known that credit card fraud goes un-caught quite often. This model predicts that only about 2.7% of domestic credit card fraud crimes lead to an arrest. Other sources predict less than 1%, but regardless this is probability a realistic estimate. (Reference 2)

IV.B Identifying states with the lowest rate of fraud

In the following table, we see the ranking of the states with the lowest probability of a person comitting a fraudulent act (one of the crimes in the listing above). We also see the estimated percentage for which arrests are made for these crimes.

rank	states	fraud probability	%est.Caught
1	CONNECTICUT	0.0186	21.03
2	VERMONT	0.0286	6.46
3	MASSACHUSETTS	0.0297	11.43
4	PENNSYLVANIA	0.0297	15.77
5	RHODE ISLAND	0.0378	9.82

IV.C Nationwide heatmap representations

In the following plots, we see nationwide heatmaps of some interesting statistics. In the first, we have a distribution of the probability of a person comitting fraud from each state. If a state is white, it was not present in the data set. These are plotly plots, so click each graph for better interactivity!

In this next plot, we see an estimation on the percentage at which fraud crimes lead to an arrest.

And in this last heat plot, we have the probability of a person in each state comitting any crime.

IV.D Overall Distribution of crimes and frauds

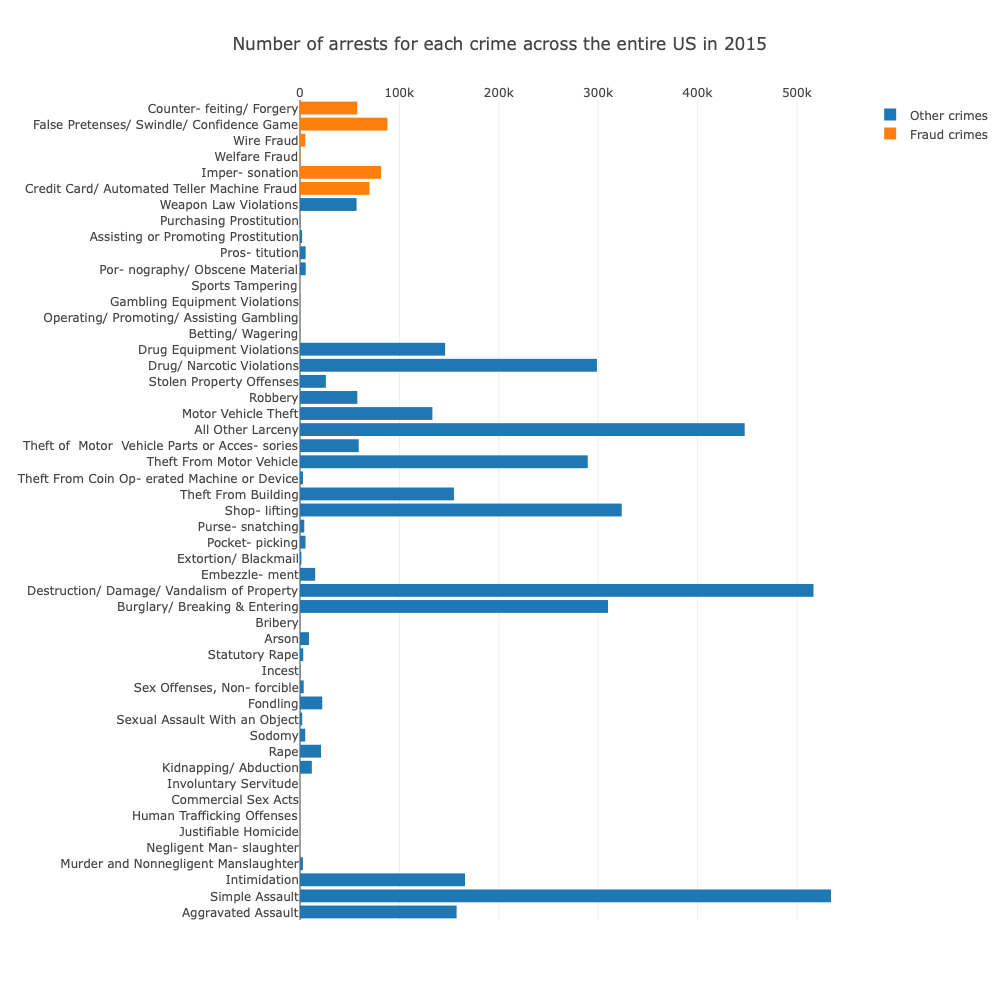
It's also good to see the overall distribution of crimes that were recorded, as well as the break down of frauds. These can be represented by bar charts and pie charts. Keep in mind these numbers were extracted from a population of 60.1Million people.

In this next chart, we have the counts of each type of crime recorded in the data set. Out of the 60.1 million people included in the data, there were 4.1 million arrests.

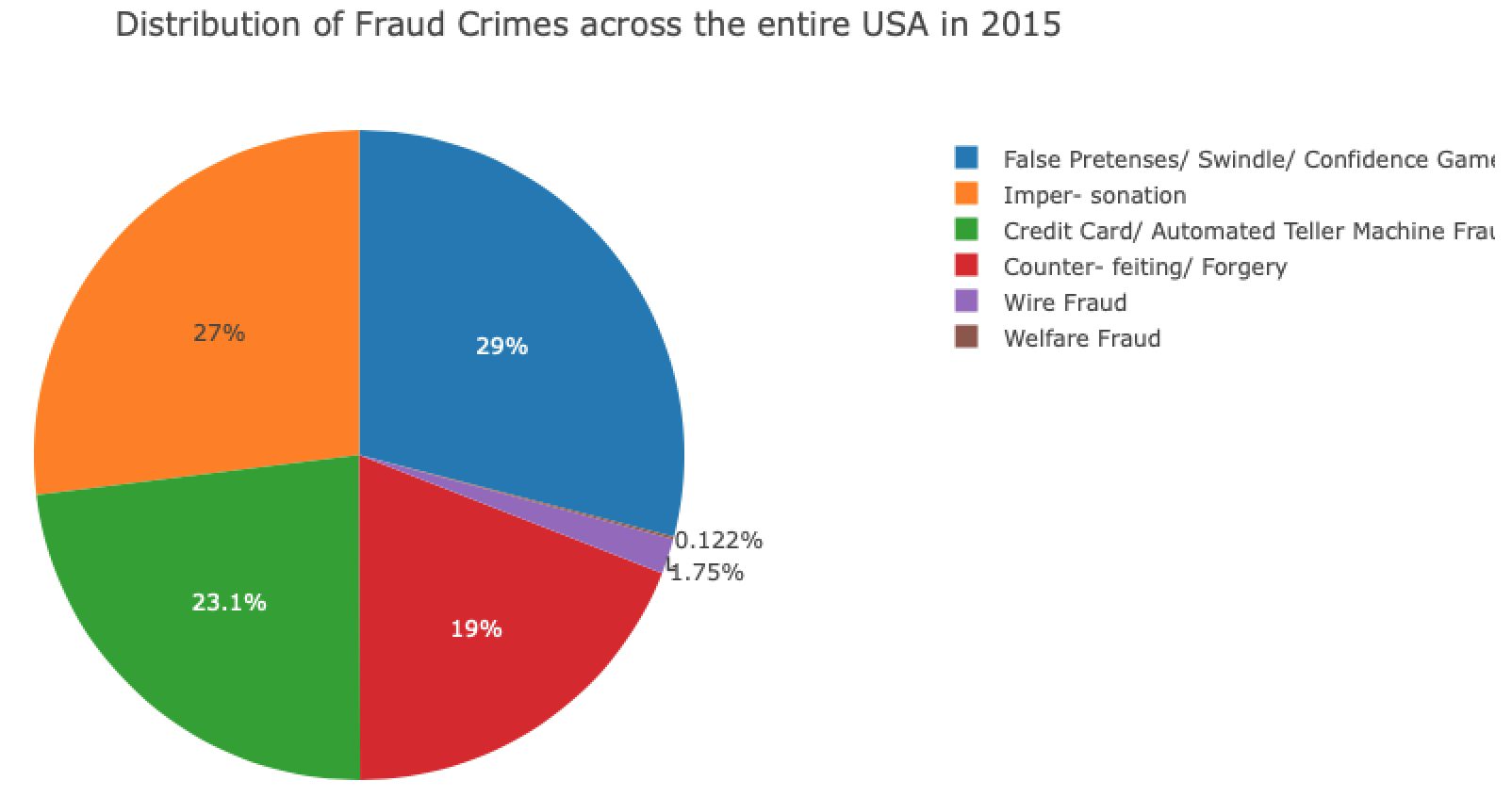
And finally, we have a pie chart break down of the different types of frauds present. There were a total of 302,783arrests for fraud related crimes (about 7.4% of all crimes).

V. Conclusions¶

Using the model and the data we can draw a few conclusions;

The states with the lowest chance of someone comitting a fraud crime are (1-3%)
1. CONNECTICUT
2. VERMONT
3. MASSACHUSETTS
4. PENNSYLVANIA
5. RHODE ISLAND
It was noticed that these states also had higher rates of arrests for fraud crimes (6-21% of cases lead to an arrest)
Crime rates were also low in these states to (3-5%)
The probability of a person comitting a fraud crime varies from (1% to 17%) across the USA
The top four types of frauds that people get arrested for are
- Swindling (29%)
- Impersonation (27%)
- Credit card fraud (23.1%)
- Counterfitting (19%)
Fraud crimes consist of about 7% of all crimes.
About 2.7% of credit card frauds lead to an arrest.